Sindhi Media
سينيئر رڪن
ٽرانسفارمر ٺاهڻ لا فارمولا جو استعمال۽ ضرورت
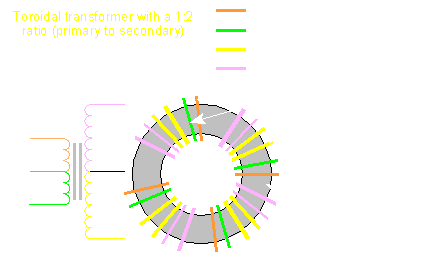

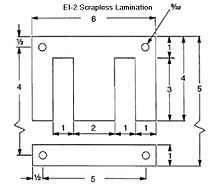

There are two approaches used in designing transformers. One uses the long formulas, and the other uses the Wa product. The Wa product is simply the cores window area multiplied by the cores area. Some say it simplifies the design, especially in C-core (cut core) construction. Most manufacturers of C-cores have the Wa product added into the tables used in their selection. The designer takes the area used by a coil and finds a C-core with a similar window area. The Wa product is then divided by the window area to find the area of the core. Either way will bring the same result.




There are two approaches used in designing transformers. One uses the long formulas, and the other uses the Wa product. The Wa product is simply the cores window area multiplied by the cores area. Some say it simplifies the design, especially in C-core (cut core) construction. Most manufacturers of C-cores have the Wa product added into the tables used in their selection. The designer takes the area used by a coil and finds a C-core with a similar window area. The Wa product is then divided by the window area to find the area of the core. Either way will bring the same result.
انتظامي رڪن طرفان آخري ترميم: