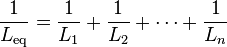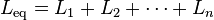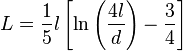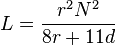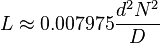Sindhi Media
سينيئر رڪن
اچو ته اليڪٽرانڪس دُنيا جي ٽئين چيف ڪمپونينٽ (ڪوائل يا انڊڪٽر) تي ڪم ڪريون ۽ سمجهون



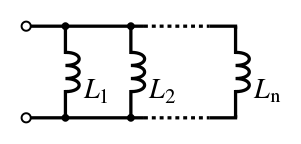
انڊڪٽر يا ڪوائل کي ري ايڪٽر به چئبو آهي۔ هي بُنيادي طرح( پيسوِ 2 الرڪٽروڊ) ڪمپونينٽ هوندو آهي۔ جنهن جو ڪم پاڻ مان پاس ٿيندڙ اليڪٽرڪ يا اليڪٽرانڪ وهڪري (ڪرنٽ) جي تبديلي يا (چينجز) کي رڪاوٽ (رازسٽس) ڪرڻ آهي۔ هي جنهن ڪنڊڪٽر تي مشتمل هوندو آهي اها محض هڪ تار هوندي آهي جنهن کي گولائي ۾ ويڙهبو آهي جيڪو ڪوائل بڻجي ويندو آهي۔ ڪرنٽ جي وهڻ سان اُن ڪوائل جي چوڌاري هڪ انرجي پئدا ٿيندي آهي جنهن کي مئگنيٽ (مقناطيسي) فيلڊ چئبو آهي ۔ جڏنهن ان انڊڪٽر مان ڪرنٽ چينجز ، سان ٽائيم ويرينگ (وقت تبديل ٿيندڙ) مئگنيڪٽڪ فيلڊ ان ڪنڊڪٽر ۾ وولٽيج کي پئدا ڪندي آهي ۽Faraday’s law of electromagnetic induction, موجب اهان ان ڪرنٽ وهڻ جي مخالفت ڪندي آهي جيڪو ان ۾ پئدا ٿيندو آهي۔



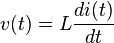




انڊڪٽر يا ڪوائل کي ري ايڪٽر به چئبو آهي۔ هي بُنيادي طرح( پيسوِ 2 الرڪٽروڊ) ڪمپونينٽ هوندو آهي۔ جنهن جو ڪم پاڻ مان پاس ٿيندڙ اليڪٽرڪ يا اليڪٽرانڪ وهڪري (ڪرنٽ) جي تبديلي يا (چينجز) کي رڪاوٽ (رازسٽس) ڪرڻ آهي۔ هي جنهن ڪنڊڪٽر تي مشتمل هوندو آهي اها محض هڪ تار هوندي آهي جنهن کي گولائي ۾ ويڙهبو آهي جيڪو ڪوائل بڻجي ويندو آهي۔ ڪرنٽ جي وهڻ سان اُن ڪوائل جي چوڌاري هڪ انرجي پئدا ٿيندي آهي جنهن کي مئگنيٽ (مقناطيسي) فيلڊ چئبو آهي ۔ جڏنهن ان انڊڪٽر مان ڪرنٽ چينجز ، سان ٽائيم ويرينگ (وقت تبديل ٿيندڙ) مئگنيڪٽڪ فيلڊ ان ڪنڊڪٽر ۾ وولٽيج کي پئدا ڪندي آهي ۽Faraday’s law of electromagnetic induction, موجب اهان ان ڪرنٽ وهڻ جي مخالفت ڪندي آهي جيڪو ان ۾ پئدا ٿيندو آهي۔




انتظامي رڪن طرفان آخري ترميم: